BIP: 360
  Title: Pay to Quantum Resistant Hash
  Layer: Consensus (soft fork)
  Author: Hunter Beast <hunter@surmount.systems>
          Ethan Heilman <ethan.r.heilman@gmail.com>
  Comments-Summary: No comments yet.
  Comments-URI: https://github.com/bitcoin/bips/wiki/Comments:BIP-0360
  Status: Draft
  Type: Standards Track
  Created: 2024-12-18
  License: BSD-3-Clause

Introduction

Abstract

This document proposes the introduction of a new output type, Pay to Quantum Resistant Hash (P2QRH), via a soft fork. P2QRH provides the same tapscript functionality as Pay to TapRoot (P2TR) but removes the quantum-vulnerable key-spend path in P2TR. By itself, P2QRH provides protection against long-exposure quantum attacks, but requires PQ signatures to provide full security against Cryptanalytically-Relevant Quantum Computing (CRQCs). P2QRH is designed to provide the foundation necessary for a future soft fork activating PQ signature verification in tapscript.

Copyright

This document is licensed under the 3-clause BSD license.

Motivation

The primary threat to Bitcoin from Cryptanalytically-Relevant Quantum Computing (CRQCs) A Cryptoanalytically-Relevant Quantum Computer is an object which is only loosely defined by characteristics in quantum physics as of today. It could be understood in the context of this BIP and in bitcoin that it's a hardware-agnostic computer supposed to have the architecture to keep coherent a sufficient number of logical qubits to be able to run the Shor algorithm in an efficient fashion. is their potential to break the cryptographic assumptions of Elliptic Curve Cryptography (ECC), which secures Bitcoin's signatures and Taproot commitments. Specifically, Shor's algorithm enables a CRQC to solve the Discrete Logarithm Problem (DLP) exponentially faster than classical methodsShor's algorithm is believed to need 10^8 operations to break a 256-bit elliptic curve public key., allowing the derivation of private keys from public keys-- a process referred to here as quantum key decryption. Meaning, deriving private keys from public keys via Shor's algorithm Importantly, simply doubling the public key length (e.g., using a hypothetical secp512k1 curve) would only make deriving the private key twice as hard, offering insufficient protection. The computational complexity of this attack is further explored in The impact of hardware specifications on reaching quantum advantage in the fault-tolerant regime.

This proposal aims to mitigate these risks by introducing a Pay to Quantum Resistant Hash (P2QRH) output type that makes tapscript quantum resistant and enables the use of PQ signature algorithms. By adopting PQC, Bitcoin can enhance its quantum resistance without requiring a hard fork or block size increase.

The vulnerability of existing Bitcoin addressesA vulnerable Bitcoin address is any scriptPubKey type that exposes an elliptic curve public key as raw bytes in a block, making it susceptible to private key derivation through Shor's algorithm. This includes P2PK outputs and any script that contains an unprotected public key. is detailed in this Deloitte report. The report estimates that in 2020 approximately 25% of the Bitcoin supply is held within addresses vulnerable to quantum attack. As of the time of writing, that number is now closer to 20%. Independently, Bitcoin developer Pieter Wuille reasons even more addresses might be vulnerable, representing 5M to 10M bitcoin.

Ordinarily, when a transaction is signed, the public key is explicitly stated in the input script. This means that the public key is exposed on the blockchain when the transaction is spent, making it vulnerable to quantum attack until it's mined. One way to mitigate this is to submit the transaction directly to a mining pool, bypassing the mempool. This process is known as an out-of-band transaction or a private mempool. In this case, the mining pool must be trusted not to reveal the transaction public key to attackers. The problem with this approach is that it requires a trusted third party, which the P2QRH proposal aims to avoid. It also doesn't account for block reorg attacks, which would reveal public keys in blocks that were once mined but are now orphaned and must be mined again. Additionally, it depends on the mining pool whether they reveal their block template to either the public or to miners.

Not having public keys exposed on-chain is an important step for quantum security. Otherwise, funds would need to be spent to new addresses on a regular basis in order to prevent the possibility of a "long-exposure CRQC attack" recovering the key behind high-value addresses. A long-exposure quantum attack can be considered one performed with chain data, such as that from a used address or one encoded in a spend script. This is likely to be more common early on, as early quantum computers must be run for longer in order to overcome errors caused by noise. A "short-exposure quantum attack" would be one performed on keys in the mempool, which is seen as much more difficult given the block time, and so it requires more sophisticated CRQCs. In the paper How to compute a 256-bit elliptic curve private key with only 50 million Toffoli gates the authors estimate that a CRQC with 28 million superconducting physical qubits would take 8.3 seconds to calculate a 256-bit key, while a CRQC with 6.9 million physical qubits would take 58 seconds. This implies that a CRQC with 4x as many qubits would be roughly 7 times faster.

As the value being sent increases, so too should the fee in order to commit the transaction to the chain as soon as possible. Once the transaction is mined, it makes useless the public key revealed by spending a UTXO, so long as it is never reused.

As the first step to address these issues we propose Pay to Quantum Resistant Hash (P2QRH), an output type that allows tapscript to be used in a quantum resistant manner. This new output type protects transactions submitted to the mempool and helps preserve the fee market by preventing the need for private, out-of-band mempool transactions.

The following table is intended to inform the average Bitcoin user whether their bitcoin is vulnerable to a long-exposure quantum attack:

¹ Funds in P2PKH, P2SH, P2WPKH, and P2WSH outputs become vulnerable to long-exposure quantum attacks when their input script is revealed. An address is no longer safe against long-exposure quantum attacks after funds from it have been spent.

It should be noted that Taproot outputs are vulnerable in that they encode a 32-byte x-only public key, from which a full public key can be reconstructed.

If a CRQC recovers an extended public key (xpub), including its chain code, it can derive all non-hardened child public keys by guessing or iterating through child indexes, as allowed by BIP-32's non-hardened derivation. With Shor's algorithm, the CRQC could then compute the corresponding non-hardened child private keys directly from those public keys, without needing the extended private key (xprv) or an exposed child private key. Hardened child keys remain secure since they cannot be derived from the xpub alone. However, if the xprv is exposed, then all child private keys--both hardened and non-hardened--become vulnerable. Thus, in a quantum context, the xpub alone is sufficient to expose all non-hardened child private keys.

Long Exposure and Short Exposure Quantum Attacks

A Long Exposure Quantum Attack is an attack in which the public key has been exposed on the blockchain for an extended period of time, giving an attacker ample opportunity to break the cryptography. This affects:

• P2PK outputs (Satoshi's coins, CPU miners, starts with 04)
• Reused addresses (any type, except P2QRH)
• Taproot addresses (starts with bc1p)
• Extended public keys, commonly known as "xpubs"
• Wallet descriptors

A Short Exposure Quantum Attack is an attack that must be executed quickly while a transaction is still in the mempool, before it is mined into a block. This affects:

• Any transaction in the mempool (except for P2QRH)

Short-exposure attacks require much larger, more expensive CRQCs since they must be executed within the short window before a transaction is mined. Long-exposure attacks can be executed over a longer timeframe since the public key remains exposed on the blockchain indefinitely.

Coinbase outputs to P2PK keys go as far as block 200,000, so there are, at the time of writing, 1,723,848 coins that are vulnerable from the first epoch in P2PK outputs alone. The majority of these have a block reward of 50 coins each, and there are roughly 34,000 distinct P2PK scripts that are vulnerable. These coins can be considered "Satoshi's Shield." Any addresses with a balance of less than the original block subsidy of 50 coins can be considered cryptoeconomically incentive incompatible to capture until all of these are mined, and these addresses serve to provide time to transition Bitcoin to implement post-quantum security.

It's for the above reason that, for those who wish to be prepared for quantum emergency, it is recommended that no more than 50 bitcoin are kept under a single, distinct, unused Native SegWit (P2WPKH, "bc1q") address at a time. This is assuming that the attacker is financially motivated instead of, for example, a nation state looking to break confidence in Bitcoin. Independently, this assumes that other vulnerable targets such as central banks have upgraded their cryptography by this time.

The Commercial National Security Algorithm Suite (CNSA) 2.0 has a timeline for software and networking equipment to be upgraded by 2030, with browsers and operating systems fully upgraded by 2033. According to NIST IR 8547, Elliptic Curve Cryptography is planned to be disallowed within the US federal government after 2035. An exception is made for hybrid cryptography, which is the use of ECC and post-quantum algorithms together.

Although the main threat posed by CRQCs is to the signatures used in Bitcoin, a smaller threat is to Bitcoin's hash algorithms. In particular, while a CRQC could use Grover's algorithm to gain a quadratic speedup on brute-force attacks on the hash functions used in Bitcoin, a significantly more powerful CRQC is needed for these attacks to meaningfully impact Bitcoin. For instance, a preimage attack on HASH160 Used by P2PKH, P2SH, and P2WPKH addresses, though not P2WSH because it uses 256-bit hashes. using Grover's algorithm would require at least 10^24 quantum operations. As for Grover's application to mining, see Sam Jaques' post on this.

Design

This is the first in a series of BIPs under a QuBit soft fork. A qubit is a fundamental unit of quantum computing, and the capital B refers to Bitcoin. The name QuBit also rhymes to some extent with SegWit. This BIP proposes a new output type called P2QRH (Pay to Quantum Resistant Hash). This output type is designed to support post-quantum signature algorithms but those algorithms will be specified in future BIPs.

It is proposed to use SegWit version 3. This results in addresses that start with bc1r, which could be a useful way to remember that these are quantum (r)esistant addresses. This is referencing the lookup table under BIP-173.

P2QRH (Pay to Quantum Resistant Hash) is a new output type that commits to the root of a tapleaf merkle tree. It is functionally the same as a P2TR (Pay to Taproot) output with the quantum vulnerable key-spend path removed. Since P2QRH has no key-spend path, P2QRH omits the taproot internal key as it is not needed. Instead a P2QRH output is just the 32 byte root of the tapleaf merkle tree as defined in BIP-341 and hashed with the tag "QuantumRoot" as shown below.

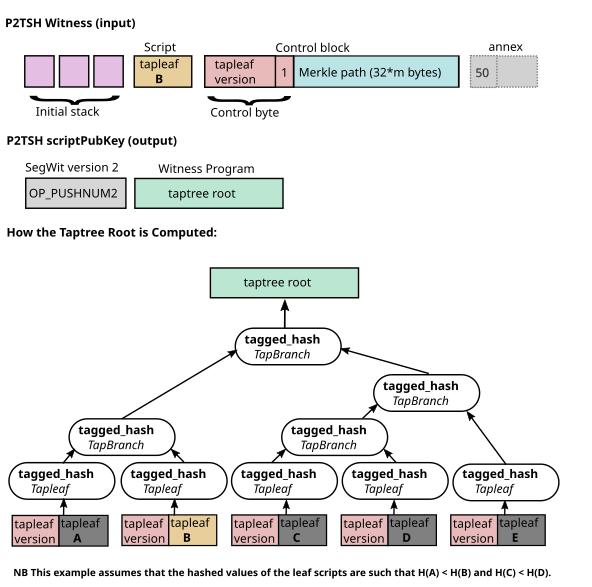
To construct a P2QRH output we follow the same process as BIP-341 to compute the tapscript merkle root. However, instead of the root of the Merkle tree being hashed together with the internal key in P2QRH the root is hashed by itself using the tag "QuantumRoot".

D = tagged_hash("TapLeaf", bytes([leaf_version]) + ser_script(script))
CD = tagged_hash("TapBranch", C + D)
CDE = tagged_hash("TapBranch", E + CD)
ABCDE = tagged_hash("TapBranch", AB + CDE)
Root = tagged_hash("QuantumRoot", ABCDE)

A P2QRH input witness provides the following:

initial stack element 0,
...,
initial stack element N,
tapleaf script,
control block = [control byte, 32 * m byte Merkle path] # m is the depth of the Merkle tree

The initial stack elements provide the same functionality as they do in P2TR. That is, they place elements on the stack to be evaluated by the tapleaf script, a.k.a. the redeem script.

The control block is a 1 + 32 * m byte array, where the first byte is the control byte and the next 32*m bytes are the Merkle path to the tapleaf script. The control byte is the same as the control byte in a P2TR control block, including the 7 bits are used to specify the tapleaf version. The parity bit of the control byte is always 1 since P2QRH does not have a key-spend path. We omit the public key from the control block as it is not needed in P2QRH. We maintain support for the optional annex in the witness (see specification for more details).

Rationale

Our design to augment Bitcoin with quantum resistance is guided by the following principles:

Minimize changes. We should reuse existing Bitcoin code and preserve existing software behavior, workflows, user expectations and compatibility whenever possible.

Gradual upgrade path. We should provide an upgrade path for wallets and exchanges which can be carried out gradually and iteratively rather than all at once. This is critical as the earlier the ecosystem begins upgrading to quantum resistance, the lower the number of coins at risk when quantum attacks become practical.

Use standardized post-quantum signature algorithms. Standardized algorithms have undergone the most scrutiny and are likely to be most well supported and well studied going forward. The entire Bitcoin ecosystem will benefit from using the most popular post-quantum signature algorithms, including leveraging hardware acceleration instructions, commodity trusted hardware, software libraries and cryptography research.

Provide security against unexpected cryptanalytic breakthroughs. Consider the risk if Bitcoin only supported one PQ signature algorithm, and then following the widespread rollout of CRQCs, a critical weakness is unexpectedly discovered in this signature algorithm. There would be no safe algorithm available. We believe that prudence dictates we take such risks seriously and ensure that Bitcoin always has at least two secure signature algorithms built on orthogonal cryptographic assumptions. In the event one algorithm is broken, an alternative will be available. An added benefit is that parties seeking to securely store bitcoins over decades can secure their coins under multiple algorithms, ensuring their coins will not be stolen even in the face of a catastrophic break in one of those signature algorithms.

Based on these principles, we propose two independent changes that together provide Bitcoin with full quantum resistance. In this BIP, we introduce a new output type called P2QRH (Pay to Quantum Resistant Hash) so that tapscript can be used in a quantum resistant manner. In a future BIP, we enable tapscript programs to verify two Post-Quantum (PQ) signature algorithms, ML-DSA (CRYSTALS-Dilithium) and SLH-DSA (SPHINCS+). It is important to consider these two changes together because P2QRH must be designed to support the addition of these PQ signature algorithms. The full description of these signatures will be provided in a future BIP.

P2QRH

P2QRH is simply P2TR with the quantum vulnerable key-spend path removed so that it commits to the root of the tapleaf merkle tree in the output. This allows P2QRH to reuse the mature and battle tested P2TR, tapleaf and tapscript code already in Bitcoin. This reduces the implementation burden on wallets, exchanges, and libraries since they can reuse code they already have.

Both P2WSH (Pay 2 Witness Script Hash) and P2QRH protect against long-exposure quantum attacks and both provide the same 256-bit security level. One may ask why not use the existing output type P2WSH instead of add a new one? The problem with P2WSH is that it only works with pre-tapscript Script and cannot work with tapscript Script. New protocols and programs in the Bitcoin ecosystem have largely moved to tapscript. Using P2WSH would require turning back the clock and forcing projects to move from tapscript to pre-tapscript. More importantly, tapscript provides a far easier and safer upgrade path for adding PQ signatures. Changes to pre-tapscript to enable it to support PQ signatures would likely require adding tapscript features into pre-tapscript. Even if this was possible, it would represent far more work and risk than adding a new output type like P2QRH. Tapscript, and thereby a tapscript compatible output such as P2QRH, is the most plausible and convenient upgrade path to full quantum resistance.

PQ signatures

By separating P2QRH from the introduction of PQ signatures, relying parties can move from P2TR to P2QRH without simultaneously having to change from Schnorr signatures to PQ signatures. Simply moving coins from P2TR to P2QRH protects those coins from long-exposure quantum attacks. Then to gain full quantum resistance, verification of PQ signatures can be added as an additional tapleaf alongside Schnorr signaturesMatt Corallo, Trivial QC signatures with clean upgrade path, (2024). When quantum attacks become practical, users would then be fully protected as the P2QRH output would allow them to switch to sending their coins using the PQ signature algorithms. This allows the upgrade to quantum resistance to be largely invisible to users.

Consider the P2QRH output with three tapscripts:

• Spend requires a Schnorr signature
• Spend requires a ML-DSA signature
• Spend requires a SLH-DSA signature

In the event that Schnorr signatures are broken, users can spend their coins using ML-DSA. If both Schnorr and ML-DSA are broken, the user can still rely on SLH-DSA. While this pattern allows users to spend their coins securely without revealing the public keys associated with vulnerable algorithms, the user can compromise their own security if they leak these public keys in other contexts, e.g. key reuse.

One intent in supporting Schnorr, ML-DSA, and SLH-DSA in tapscript, is to allow parties to construct outputs such that funds are still secure even if two of the three the signature algorithms are completely broken. This is motivated by the use case of securely storing Bitcoins in a cold wallet for very long periods of time (50 to 100 years).

For PQ signatures we considered the NIST approved SLH-DSA (SPHINCS+), ML-DSA (CRYSTALS-Dilithium), FN-DSA (FALCON). Of these three algorithms, SLH-DSA has the largest signature size, but is the most conservative choice from a security perspective because SLH-DSA is based on well studied and time-tested hash-based cryptography. Both FN-DSA and ML-DSA signatures are significantly smaller than SLH-DSA signatures but are based on newer lattice-based cryptography. Since ML-DSA and FN-DSA are both similar lattice-based designs, we choose to only support one of them as the additional value in diversity of cryptographic assumptions would be marginal. It should be noted that ML-DSA and FN-DSA do rely on different lattice assumptions and it may be that case that a break in one algorithm's assumptions would not necessarily break the assumptions used by the other other algorithm.

We also considered SQIsign. While it outperforms the three other PQ signature algorithms by having the smallest signatures, it has the worst verification performance and requires a much more complex implementation. We may revisit SQIsign separately in the future as recent research shows massive performance improvements to SQIsign in version 2.0. "[SQIsign] signing is now nearly 20× faster, at 103.0 Mcycles, and verification is more than 6× faster, at 5.1 Mcycles" SQIsign: Algorithm specifications and supporting documentation Version 2.0 (February 5 2025).

ML-DSA is intended as the main PQ signature algorithm in Bitcoin. It provides a good balance of security, performance and signature size and is likely to be the most widely supported PQ signature algorithm on the internet. SLH-DSA has a radically different design and set of cryptographic assumptions than ML-DSA. As such SLH-DSA provides an effective hedge against an unexpected cryptanalytic breakthrough.

P2QRH, ML-DSA, and SLH-DSA could be activated simultaneously in a single soft fork or P2QRH could be activated first and then ML-DSA and SLH-DSA could be independently activated. If at some future point another signature algorithm was desired it could follow this pattern.

We consider two different paths for activating PQ signatures in Bitcoin. The first approach is to redefine OP_SUCCESSx opcodes for each signature algorithm. For ML-DSA this would give us OP_CHECKMLSIG, OP_CHECKMLSIGVERIFY and OP_CHECKMLSIGADD. The second approach is to use a new tapleaf version that changes the OP_CHECKSIG opcodes to support the new PQ signature algorithms. In both cases, we would need to include as part of the soft fork an increase in the tapscript stack element size to accommodate the larger signatures and public keys sizes of the PQ signature algorithms.

The OP_SUCCESSx approach has the advantage of providing a straightforward path to add new signature algorithms in the future. Simply redefine a set of five OP_SUCCESSx opcodes for the new signature algorithm. This would allow us to activate a single PQ signature at a time, adding new ones as needed. Additionally this approach allows developers to be very explicit in the signature algorithm type that they wish to verify. The main disadvantage is that it uses five OP_SUCCESSx opcodes per signature algorithm. Supporting ML-DSA and SLH-DSA would require ten new opcodes.

Adding PQ signatures via a tapleaf version increase does not introduce any new opcodes and allows previously written tapscript programs to be used with PQ signatures by simply using the new tapleaf version. Instead of developers explicitly specifying the intended signature algorithm through an opcode, the algorithm to use must be indicated within the public key or public key hash¹. The disadvantage of this approach is that it requires a new tapleaf version each time we want to add a new signature algorithm.

Both approaches must raise the stack element size limit. In the OP_SUCCESSx case, the increased size limit would only be effect for transaction outputs that use of the new opcodes. Otherwise this stack element size limit increase would be a soft fork. If the tapleaf version is used, then the stack element size limit increase would apply to any tapscript program with the new tapleaf version.

To improve the viability of the activation client and adoption by wallets and libraries, a library akin to libsecp256k1 will be developed. This library, libbitcoinpqc, will support the new PQ signature algorithms and can be used as a reference for other language-native implementations.

PQ signature size

Post-quantum public keys are generally larger than those used by ECC, depending on the security level. Originally BIP-360 proposed NIST Level V, 256-bit security, but this was changed to NIST Level I, 128-bit security due to concerns over the size of the public keys, the time it would take to verify signatures, and being generally deemed "overkill".

We recognize that the size of ML-DSA (CRYSTALS-Dilithium) and SLH-DSA (SPHINCS+) signatures + public key pairs is a significant concern. By way of comparison with Schnorr public key + signature pairs, SLH-DSA is roughly 80x larger and ML-DSA is roughly 40x larger. This means to maintain present transaction throughput, an increase in the witness discount may be desired.

An increase in the witness discount must not be taken lightly. Parties may take advantage of this discount for purposes other than authorizing transactions (e.g., storage of arbitrary data as seen with "inscriptions"). An increase in the witness discount would not only impact node runners but those with inscriptions would have the scarcity of their non-monetary assets affected.

There was some hope of designing P2QRH such that discounted public keys and signatures could not be repurposed for the storage of arbitrary data by requiring that they successfully be verified before being written to Bitcoin's blockchain, a.k.a. "JPEG resistance". Later research ² provided strong evidence that this was not a feasible approach for the NIST approved Post-Quantum signature algorithms. It is an open question if Post-Quantum signature algorithms can be designed to provide JPEG resistance.

Raising tapscript's stack element size

A problem faced by any attempt to add PQ signatures to tapscript is that the stack elements in tapscript cannot be larger than 520 bytes because the MAX_SCRIPT_ELEMENT_SIZE=520. This is problematic because PQ signature algorithms often have signatures and public keys in excess of 520 bytes. For instance:

• ML-DSA public keys are 1,312 bytes and signatures are 2,420 bytes
• SLH-DSA public keys are 32 bytes and signatures are 7,856 bytes

We will first look at our approach to the problem of PQ signatures and then give our solution for public keys larger than 520 bytes.

To keep P2QRH small and simple, we have opted not to raise the stack element size limit as part of P2QRH, but instead make this change when adding of PQ signatures. That said, we are not strongly opposed to putting this increase in P2QRH.

We propose a stack element size limit of 8,000 bytes. We arrive at 8,000 by rounding up from the needed 7,856 bytes.

OP_DUP will duplicate any stack element. Thus, if we allowed OP_DUP to duplicate stack elements of size 8,000 bytes, it would be possible to write a tapscript which will duplicate stack elements until it reaches the maximum number of elements on stack, i.e. 1000 elements. An increase from 520 bytes to 8,000 bytes would increase the memory footprint from 520 KB to 8 MB.

To prevent OP_DUP from creating an 8 MB stack by duplicating stack elements larger than 520 bytes we define OP_DUP to fail on stack elements larger than 520 bytes. Note this change to OP_DUP is not consensus critical and does not require any sort of fork. This is because currently there is no way to get a stack element larger than 520 bytes onto the stack so triggering this rule is currently impossible and would only matter if the stack element size limit was raised.

Public keys larger than 520 bytes

Turning our attention to public keys larger than 520 bytes. This is not needed for SLH-DSA as its public key is only 32 bytes. This is a different problem than signatures as public keys are typically pushed onto the stack by the tapleaf script (redeem script) to commit to public keys in output. The OP_PUSHDATA opcode in tapscript fails if asked to push more than 520 bytes onto the stack.

To solve this issue, for signature schemes with public keys greater than 520 bytes, we use the hash of the public key in the tapleaf script. We then package the public key and signature together as the same stack element on the input stack. Since the hash of the public key is only 32 bytes, the tapleaf script can push it on the stack as it does today. Consider the following example with a OP_CHECKMLSIG opcode for ML-DSA:

stack = [pubkey||signature]
tapscript = [OP_PUSHDATA HASH256(expected_pubkey), OP_CHECKMLSIG]

1. OP_PUSHDATA HASH256(expected_pubkey) updates the stack to pubkey||signature
2. OP_CHECKMLSIG pops HASH256(expected_pubkey) and pubkey||signature, checks HASH256(expected_pubkey) == pubkey and verifies signature against pubkey.

Future considerations

Additional follow-on BIPs will be needed to implement PQ signature algorithms, signature aggregation, and full BIP-32 compatibility (if possible) BIP-32 relies on elliptic curve operations to derive keys from xpubs to support watch-only wallets, which PQC schemes may not support.. However, until specialized quantum cryptography hardware is widespread and signature aggregation schemes are thoroughly vetted, P2QRH addresses are an intermediate solution to quantum threats.

Specification

We define the Pay to Quantum Resistant Hash (P2QRH) output structure as follows.

Pay to Quantum Resistant Hash (P2QRH)

A P2QRH output is simply the root of the tapleaf Merkle tree defined in BIP-341 and used as an internal value in P2TR.

To construct a P2QRH output we follow the same process as BIP-341 to compute the tapscript merkle root. However, instead of the root of the Merkle tree being hashed together with the internal key in P2QRH the root is hashed by itself using the tag "QuantumRoot" and then set as the witness program.

Address Format

P2QRH uses SegWit version 3 outputs, resulting in addresses that start with bc1r, following BIP-173. Bech32 encoding maps version 3 to the prefix r.

Example P2QRH address:

bc1r... (32-byte Bech32m-encoded tapleaf merkle root)

ScriptPubKey

The scriptPubKey for a P2QRH output is:

  OP_PUSHNUM_3 OP_PUSHBYTES_32 <nowiki><hash></nowiki>

Where:

• OP_PUSHNUM_3 (0x53) indicates SegWit version 3.
• is the 32-byte tapleaf merkle root.

Script Validation

A P2QRH output is a native SegWit output (see BIP141) with version number 3, and a 32-byte witness program. Unlike taproot this witness program is the tapleaf merkle root. For the sake of comparison we have, as much as possible, copied the language verbatim from the BIP341 script validation section.

• Let q be the 32-byte array containing the witness program (the second push in the scriptPubKey) which represents root of tapleaf merkle tree.
• Fail if the witness stack does not have two or more elements.
• If there are at least three witness elements, and the first byte of the last element is 0x50, this last element is called annex a and is removed from the witness stack. The annex (or the lack of thereof) is always covered by the signature and contributes to transaction weight, but is otherwise ignored during taproot validation.
• There must be at least two witness elements left.
  • Call the second-to-last stack element s, the script (as defined in BIP341)
  • The last stack element is called the control block c, and must have length 1 + 32 * m, for a value of m that is an integer between 0 and 128, inclusive. Fail if it does not have such a length.
  • Let v = c[0] & 0xfe be the leaf version (as defined in BIP-341). To maintain leaf version encoding compatibility the last bit of c[0] is unused and must be 1 ³.
  • Let k₀ = hash_TapLeaf(v || compact_size(size of s) || s); also call it the tapleaf hash.
  • For j in [0,1,...,m-1]:
    • Let e_j = c[33+32j:65+32j].
    • Let _k_j+1 depend on whether k_j < e_j (lexicographically): * If k_j < e_j: k_j+1 = hash_TapBranch(k_j || e_j). * If k_j ≥ e_j: k_j+1 = hash_TapBranch(e_j || k_j).
  • Let r = hash_QuantumRoot(k_m).
  • If q ≠ r, fail.
  • Execute the script, according to the applicable script rules, using the witness stack elements excluding the script s, the control block c, and the annex a if present, as initial stack. This implies that for the future leaf versions (non-0xC0) the execution must succeed.

The steps above follow the script path spending logic from BIP-341 with the following changes:

• The witness program is the tapleaf merkle root and not a public key. This means that we skip directly to BIP-341 spend path tapleaf merkle tree validation.
• We compute the tagged tapleaf merkle root r and compare it directly to the witness program q.
• The control block is 1 + 32m bytes, instead of 33 + 32m bytes.

Sighash Calculation

The sighash for P2QRH outputs follows the same procedure as defined in BIP-341 for Taproot transactions:

• Signature Message: A single-SHA256 of a tagged hash with the tag "TapSighash", containing transaction data.
• Tagged Hash: Computed as H(tag || tag || data) where H is SHA256 and tag is the SHA256 of the tag name.
• Key Data: In addition to transaction data, the sighash includes the spent output's scriptPubKey.
• Extension Fields: Specific data is included or excluded from the sighash based on the sighash flag.

This signature hash construction ensures transaction malleability is prevented while providing flexibility through different sighash types (DEFAULT, ALL, NONE, SINGLE, and ANYONECANPAY variants). The exact computation follows the procedure specified in BIP-341 to maintain compatibility with Taproot signatures.

If a sighash flag other than DEFAULT is needed, it can be placed in the transaction witness. In this case, it will be the only field in the witness.

Compatibility with BIP-141

By adhering to the SegWit transaction structure and versioning, P2QRH outputs are compatible with existing transaction processing rules. Nodes that do not recognize SegWit version 3 will treat these outputs as anyone-can-spend but, per BIP-141, will not relay or mine such transactions.

Transaction Size and Fees

Equivalent P2QRH and P2TR outputs are always the same size. P2QRH inputs can be slightly larger or smaller than their equivalent P2TR inputs. Let's consider the cases:

P2TR key-spend P2QRH inputs will be larger than P2TR inputs when the P2TR output would have been spent via the key-spend path. P2QRH quantum resistance comes from removing the P2TR key-spend path. Consequently it cannot make use of taproot's optimization where P2TR key-spends do not require including a merkle path in the P2TR input. If the Merkle tree only has a single tapleaf, no Merkle path is needed in the control block giving us a 1 byte control block.

P2QRH witness (103 bytes):

[count] (1 byte), # Number of elements in the witness
[size] signature  (1 + 64 bytes = 65 bytes),
tapleaf script = [size] [OP_PUSHBYTES_32, 32 byte public key, OP_CHECKSIG] (1 + 1 + 32 + 1 bytes = 35 bytes),
control block = [size] [control byte]  (1 + 1 = 2 bytes)

P2TR key-spend witness (66 bytes):

[count] (1 byte), # Number of elements in the witness
[size] signature (1 + 64 bytes = 65 bytes)

Thus, the P2QRH input would be 103 - 66 = 37 bytes larger than a P2TR key-spend input.

If the Merkle tree has more than a single tapleaf, then the Merkle path must be included in the control block. P2QRH witness (103+32*m bytes)

[count] (1 byte), # Number of elements in the witness
[size] signature  (64 + 1 bytes = 65 bytes),
tapleaf script = [size] [OP_PUSHBYTES_32, 32 byte public key, OP_CHECKSIG] (34 + 1 bytes = 35 bytes),
control block = [size] [control byte, 32 * m byte Merkle path]  (1 + 1 + 32 * m = 2 + 32 * m bytes)

For a Merkle path of length m, it would add an additional ~32 * m bytes to the P2QRH input. This would make it 37 + 32 * m bytes larger than a P2TR key-spend input⁴.

Considering a P2QRH output that has a PQ signature tapleaf and a Schnorr tapleaf. The P2QRH witness to spend the Schnorr path would be 103 + 32 * 1 = 135 bytes. It is unfortunate that we can not use the key-spend optimization for P2QRH inputs, but the key-spend optimization is exactly what makes P2TR vulnerable to quantum attacks. If spend-key was quantum resistant we wouldn't need P2QRH at all.

P2TR script-spend P2QRH inputs will be smaller than equivalent script-spend path P2TR inputs. This is because P2QRH inputs do not require that the input includes a public key in the witness control block to open the commitment to the tapleaf merkle root. An equivalent P2QRH input will be 32 bytes smaller than a P2TR script-spend input.

Performance Impact

P2QRH is slightly more computationally performant than P2TR, as the operations to spending a P2QRH output is a strict subset of the operations needed to spend a P2TR output.

Backward Compatibility

Older wallets and nodes that have not been made compatible with SegWit version 3 and P2QRH will not recognize these outputs. Users should ensure they are using updated wallets and nodes to use P2QRH addresses and validate transactions using P2QRH outputs.

P2QRH is fully compatible with tapscript and existing tapscript programs can be used in P2QRH outputs without modification.

Security

P2QRH outputs provide the same tapscript functionality as P2TR outputs, but without the quantum-vulnerable key-spend path. This enables users, exchanges and other hodlers to easily move their coins from taproot outputs to P2QRH outputs and thereby protect their coins from long-exposure quantum attacks. The protection from long-exposure quantum attacks does not depend on the activation of post-quantum signatures in Bitcoin but does require that users do not expose their quantum vulnerable public keys to attackers via address reuse or other unsafe practices.

P2QRH uses a 256-bit hash output, providing 128 bits of collision resistance and 256 bits of preimage resistance. This is the same level of security as P2WSH, which also uses a 256-bit hash output.

P2QRH does not, by itself, protect against short-exposure quantum attacks, but such attacks can be mitigated by the future activation of post-quantum signatures in Bitcoin. With P2QRH hash, these would provide full quantum resistance to P2QRH outputs in Bitcoin. That said, the protection offered by resistance to long-exposure quantum attacks should not be underestimated. It is likely that the first CRQCs (Cryptographically Relevant Quantum Computers) will not be able to perform short-exposure quantum attacks.

As shown, supersingular elliptic curve quaternion isogeny signature algorithms represent the state of the art in post-quantum cryptography, beyond lattice cryptography alone, especially when key and signature length are major constraints. This makes inclusion of SQIsign attractive, however its performance is roughly 100,000 times slower than ECC, which is prohibitive in blockchain contexts. Meanwhile, SPHINCS+ and CRYSTALS-Dilithium signatures are already approved and have achieved broader community consensus. FALCON signatures are also NIST approved.

In comparison, the size of currently used signature algorithms are:

• ECDSA: 70-72 bytes
• Schnorr: 64 bytes

In comparison to inception date, secp256k1 was originally specified in 2000.

One consideration for choosing an algorithm is its maturity. secp256k1 was already 8 years old by the time it was chosen as Bitcoin's curve. Isogeny cryptography when it was first introduced was broken over a weekend.

Signature verification speed as it compares to Schnorr or ECDSA isn't seen as high a consideration as signature size due to block space being the primary fee constraint. As a P2QRH implementation materializes, a benchmark will be added for performance comparison.

An additional consideration is security level. Longer signature sizes provide more security. NIST has standardized five security levels for post-quantum cryptography. NIST security level I provides security equivalent to 128-bit keys, and security level V provides 256-bit security.

Test Vectors and Reference Code

TBD

Related Work

It is worth noting by way of comparison that [https://ethresear.ch/t/how-to-hard-fork-to-save-most-users-funds-in-a-quantum-emergency/18901 Vitalik Buterin's proposed solution] in an Ethereum quantum emergency is quite different from the approach in this BIP. His plan involves a hard fork of the chain, reverting all blocks after a sufficient amount of theft, and using STARKs based on BIP-32 seeds to act as the authoritative secret when signing. These measures are deemed far too heavy-handed for Bitcoin.

P2QRH and MAST (Merkelized Abstract Syntax Tree) BIP-114, and related BIPs BIP-116, BIP-117, share the idea of committing to a Merkle tree of scripts. While MAST was never activated, taproot BIP-341 incorporated this idea of a Merkle tree of scripts into its design. P2QRH inherits this capability from taproot because P2QRH is simply taproot with the key-spend path removed. As a result, P2QRH does have the taproot internal key or tweak key, instead P2QRH commits directly to the Merkle tree of scripts.

Below we attempt to summarize some of the ideas discussed on the Bitcoin Bitcoin-Dev that relate to P2QRH.

The idea of a taproot but with the key-spend path removed has been discussed a number of times in the Bitcoin community. OP_CAT Makes Bitcoin Quantum Secure notes that if we disable the key-spend in taproot and activated CAT BIP-347, we could achieve quantum resistance by using Lamport signatures with CAT. Lamport and WOTS (Winternitz One-Time Signatures) built from CAT are quantum resistant but are one-time signatures. This means that if you sign twice for the same public key, you leak your secret key. This would require major changes to wallet behavior and would represent a significant security downgrade. Trivial QC signatures with clean upgrade path and Re: P2QRH / BIP-360 Update discusses the idea of taproot but with the future ability to disable the key-spend path. The design of P2QRH is partly inspired by these discussions as P2QRH can be understood as P2TR without the key-spend path.

Commit-reveal schemes such as Re: Transition to post-quantum (2018) and Post-Quantum commit / reveal Fawkescoin variant as a soft fork (2025) have been proposed as a way to safely spend bitcoins if CRQCs become practical prior to Bitcoin adopting achieving quantum resistance. The essential idea is to leverage the fact that a CRQC can only learn your private key after a user has revealed their public key. Thus, Bitcoin could fork in an alternative way to spend an output that would leverage this property. Spending via commit-reveal would require two steps, first the user's commits on-chain to their public key along with a set of outputs the user wishes to spend to. Then, in reveal, the user sign and reveals their public key. While CRQC might be able to generate competing signatures it can not produce a commitment to the user's public key earlier than the user's commitment as it does not learn it until the reveal step.

Commit-reveal schemes can only be spent from and to outputs that are not vulnerable to long-exposure quantum attacks, such as P2PKH, P2SK, P2WPKH, etc... To use tapscript outputs with this system either a soft fork could disable the key-spend path of P2TR outputs or P2QRH could be used here as it does not have a key-spend path and thus is not vulnerable to long-exposure quantum attacks.

References

• Mailing list discussion
• Delving Bitcoin discussion
• Bitcoin Optech newsletter
• draft-bip-for-quantum-safe-address-format Bitcoin Optech discussion transcript

Footnotes

1. ^ Why not have CHECKSIG infer the algorithm based on signature size? Each of the three signature algorithms, Schnorr, ML-DSA, and SLH-DSA, have unique signature sizes. The problem with using signature size to infer algorithm is that spender specifies the signature. This would allow a public key which was intended to be verified by Schnorr to be verified using ML-DSA as the spender specified a ML-DSA signature. Signature algorithms are not often not secure if you can mix and match public key and signature across algorithms.
2. ^ Bas Westerbaan (2025), jpeg resistance of various post-quantum signature schemes
3. ^ Why set the last bit of c[0] to one? Consider a faulty implementation that deserializes the leaf version as c[0] rather than c[0] & 0xfe for both P2TR and P2QRH. If they test against P2QRH outputs and require that last bit is 1, this deserialization bug will cause an immediate error.
4. ^ If m >= 8, then the compact size will use 3 bytes rather than 1 byte

Changelog

To help implementors understand updates to this BIP, we keep a list of substantial changes.

• 2025-07-07 - P2QRH is now a P2TR with the vulnerable key-spend path disabled. Number of PQ signature algorithms supported reduced from three to two. PQ signature algorithm support is now added via opcodes or tapleaf version.
• 2025-03-18 - Correct inconsistencies in commitment and attestation structure. Switch from merkle tree commitment to sorted vector hash commitment. Update descriptor format.
• 2025-03-12 - Add verification times for each algorithm. 256 -> 128 (NIST V -> NIST I). Add key type bitmask. Clarify multisig semantics.
• 2025-02-23 - More points of clarification from review. Update dead link.
• 2025-01-20 - Remove SQIsign from consideration due to significant performance concerns. Refactor language from long-range attack to long-exposure so as to not be confused with the language around block re-org attacks.
• 2024-12-18 - Assigned BIP number.
• 2024-12-13 - Update to use merkle tree for attestation commitment. Update LR & SR quantum attack scenarios.
• 2024-12-01 - Add details on attestation structure and parsing.
• 2024-10-21 - Replace XMSS with CRYSTALS-Dilithium due to NIST approval and size constraints.
• 2024-09-30 - Refactor the ECC vs PoW section. Swap quitness for attestation.
• 2024-09-29 - Update section on PoW to include partial-preimage.
• 2024-09-28 - Add Winternitz, XMSS signatures, and security assumption types to PQC table. Omit NIST Level I table. Add spend script specification. Add revealed public key scenario table.
• 2024-09-27 - Initial draft proposal

Acknowledgements

This document is inspired by BIP-341, which introduced the design of the P2TR (Taproot) output type using Schnorr signatures.

Much gratitude to my co-founder, Kyle Crews for proofreading and editing, to David Croisant, who suggested the name "QuBit", and Guy Swann for pointing out the earlier name for the attestation, "quitness", was imperfect. The attestation was later discarded when Ethan Heilman joined as co-author, whom I'm incredibly grateful to for transforming this BIP into something far more congruent with existing Bitcoin design. Thank you as well to those who took the time to review and contribute, including Jeff Bride, Adam Borcany, Antoine Riard, Pierre-Luc Dallaire-Demers, Mark Erhardt, Joey Yandle, Jon Atack, Armin Sabouri, Jameson Lopp, Murchandamus, and Vojtěch Strnad.